有意水準の基礎と応用をわかりやすく解説

こんにちは。デジタルマーケティングカンパニー・オノフのmiyamotoです。
有意水準とは統計学において、仮説検定を行う際に使用される指標の一つです。具体的には、統計的な分析結果が「偶然によるものではない」と言えるかどうかを判断する基準です。多くの場合、有意水準は5%(0.05)または1%(0.01)として設定され、これが「有意である」と判定されるための基準となります。統計学の基礎から応用までを理解するためには、この有意水準の意味を正確に把握することが重要です。今回の記事では、この「有意水準」「有意差」「p値」の意味や決め方などを、わかりやすく簡単に解説します。
統計における有意水準の意味とは?
有意水準の意味について理解することは、統計分析を正しく解釈する上で非常に重要です。有意水準とは、ある観察結果が偶然で生じる確率のことを指します。言い換えれば、観察されたデータが偶然ではないと断言するための基準です。例えば、有意水準を5%に設定すると、その観察結果が偶然に起こる確率が5%以下である場合にのみ、その結果が「有意である」と判断されます。これにより、ビジネスや科学的な研究において、データに基づく意思決定がより信頼性の高いものとなります。
有意水準の定義と基本的な概念
有意水準は、統計学における仮説検定で用いられる概念で、簡単に言えば「結果が偶然であるかどうかを示す基準」です。具体的には、観察されたデータが偶然によるものである確率を判断します。例えば、有意水準が5%(0.05)に設定されている場合、観察された結果が偶然に生じる確率が5%以下であるとき、その結果は「有意である」と見なされます。このように、有意水準は統計的な信頼性を確保するための重要な指標です。
なぜ有意水準は5%なのか?その背景と理由、決め方
「なぜ有意水準は5%なのか?」という疑問が出てくると思いますが、有意水準5%が広く使われる理由は、統計学の歴史と実践的な経験に基づいています。まず、有意水準の設定は、統計学者が結果の信頼性を高めるための基準として採用してきました。5%という数値は、十分に厳格である一方、実用的な範囲内に収まるため、多くの研究分野で採用されています。さらに、5%の有意水準は、第一種過誤(誤って帰無仮説を棄却する確率)と第二種過誤(誤って対立仮説を棄却する確率)とのバランスを取るうえで都合が良いとされています。こうした背景から、有意水準5%は統計システムの標準として広く受け入れられています。
有意水準の英語表記と関連用語
有意水準の英語表記は「SignificanceLevel」です。関連する統計用語としては、「p値」(p-value)や「帰無仮説」(NullHypothesis)、「対立仮説」(AlternativeHypothesis)などがあります。p値は、観察結果が偶然に発生する確率を示す統計量で、これが有意水準と比較されます。例えば、p値が有意水準より小さい場合、観察結果は「有意である」と判断され、帰無仮説が棄却されます。これらの用語も知っておくと、統計分析の理解が一層深まります。
統計検定と有意差の理解
統計学における重要な概念の一つが統計検定です。そして、この統計検定を理解するためには、有意差やp値といった用語をわかりやすく理解することが不可欠です。統計検定では、データが偶然で得られたものであるか、何かしらの意味を持つものであるかを判断します。その際の基準となるのが有意水準であり、結果の解釈にはp値が用いられます。
p値とは何か?有意水準との比較や決め方・求め方をわかりやすく
p値とは、観察データが帰無仮説の下で得られる確率を示す指標です。言い換えると、帰無仮説を考えたときに、その結果が出る確率を意味します。具体的には、「帰無仮説が真である場合に、観察されたデータ以上の極端な結果を得る確率」を定義しています。例えば、p値が0.03であれば、観察結果が偶然に起こる確率は3%ということになります。有意水準(通常5%)と比較して、p値が有意水準より小さい場合、その結果は「有意である」とされ、帰無仮説が棄却されます。p値の計算方法は統計ソフトや手計算による方法がありますが、通常は前者が推奨されます。
有意差とは?その検定方法と意義
有意差とは、統計検定において結果が偶然ではなく、実際に意味がある差異を示していることを示す概念です。具体的には、帰無仮説(「差がない」という仮定)が棄却される際に「有意差がある」と言われます。検定方法には、t検定やカイ二乗検定、分散分析(ANOVA)などがあり、それぞれのデータセットや分析条件に適した方法を選びます。有意差の検定は、ビジネスや研究において、実際に効果があるかどうかを判断する際に非常に重要な役割を果たします。
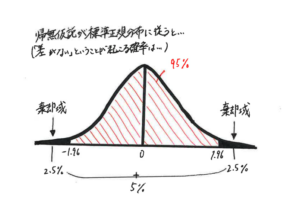
仮説検定における有意水準の役割
仮説検定とは、ある仮説(通常は帰無仮説)が正しいかどうかを統計的手法で検証するプロセスです。この検定の過程で、有意水準は重要な役割を果たします。有意水準は、観察結果が偶然である確率の上限を設定するもので、通常は5%や1%とされます。この基準に基づいて、p値が有意水準を下回る場合、帰無仮説は棄却され、「代替仮説が有力である」となります。これにより、統計検定の結果がより信頼性の高いものとなります。
有意水準の計算方法と実例
有意水準の計算方法は、統計分析において非常に重要です。一般的には統計ソフトやExcelを使用して簡単に計算できますが、その具体的な手順や理論的背景を理解することも重要です。このセクションでは、統計ソフトを用いた計算方法、Excelを使った具体例、正規分布に基づく有意水準の求め方について例題を交えて解説します。
統計ソフトを用いた有意水準の計算方法
統計ソフトを用いると、有意水準の計算が非常に効率的に行えます。代表的なソフトとしては、RやPythonの統計ライブラリ、SPSS、SASなどがあります。このようなソフトウェアは、膨大なデータセットを処理し、複雑な計算を迅速に実行するために活用されます。例えば、Rではt.test関数やanova関数を使って簡単にp値を計算し、その値を有意水準と比較して有意差の有無を確認できます。統計ソフトの使用により、手動で計算する手間を大幅に減らし、結果の信頼性を高めることが可能です。
Excelを使った具体例と解説 回帰分析
Excelは日常的に利用できるツールであり、統計分析にも応用可能です。特に回帰分析の計算方法を理解するうえで非常に便利です。例として、2つの変数間の関係を分析する場合、まずデータをExcelに入力し、”データ分析”ツールを使用して回帰分析を行います。その際、Excelは自動的にp値を計算してくれます。求められたp値が設定した有意水準(例えば5%)を下回る場合、独立変数は従属変数に対して「有意である」と判断されます。これにより、統計的に有意な関係が存在するかどうかを迅速に評価できます。

正規分布に基づく有意水準の求め方
正規分布は統計学で非常に重要な概念であり、多くの現象がこの分布に従います。有意水準の求め方も正規分布に基づいています。例えば、標準正規分布を想定すると、ある観察結果が特定の範囲内に収まる確率を計算できます。Z値(標準得点)を用いて、その観察値が正規分布のどの位置にあるかを評価し、p値を算出します。このp値を有意水準と比較して、観察結果が「有意である」かどうかを判断します。正規分布を理解することで、有意水準の設定と解釈がより確実に行えるようになります。
有意水準の設定と応用
有意水準の設定は、統計分析を行う上で非常に重要なステップです。適切に設定することで、データの解釈が正確になり、結果に基づいた信頼性のある結論を引き出すことができます。有意水準は一般的に5%や1%といった標準的な数値が用いられますが、その設定には特定の理由と目的があります。以下では、5%と1%の有意水準の違いや使い方、ビジネスにおける活用事例、さらには設定時のポイントについて詳しく解説します。
5%水準と1%水準の違いと使い方
有意水準の設定は、統計分析における重要な側面です。通常、5%水準と1%水準が一般的に使用されます。5%水準は、観察結果が偶然に起こる確率が5%以下であることを表し、p値が0.05以下であれば「有意である」とされます。これに対して、1%水準は観察結果が偶然に起こる確率がさらに低い1%以下であることを示し、p値が0.01以下であれば「1水準で有意」と判断されます。5%水準は通常の研究やビジネスの意思決定で用いられますが、有意水準1%はより厳格な基準が求められる場合(医学研究など)に使用されます。
ビジネスにおける有意差の活用事例
ビジネスの現場で統計分析を行う際、有意差の有無を確認することは非常に重要です。例えば、新製品の効果を検証するためにA/Bテストがよく用いられます。A/Bテストでは2つのバリアントを比較し、それぞれのパフォーマンスを評価します。この時、有意差が確認されれば、新製品が現行製品よりも優れていると判断できます。さらに、マーケティングキャンペーンの効果測定や顧客満足度の調査にも有意差が活用されます。これにより、データに基づく意思決定が可能となり、ビジネスの成果を最大化する方法を見つけやすくなります。
有意水準を決める際のポイントと考え方
有意水準を決める際には、いくつかのポイントと考え方を押さえる必要があります。まず、研究やビジネスの目的によって適切な有意水準が異なることを理解しておきましょう。一般的には、5%水準が標準として採用されますが、厳密さが求められる場合には1%水準が適用されます。また、有意水準の低下は結果の精度を高める一方で、第一種過誤のリスクも増えるため、バランスを考慮することが重要です。さらに、有意水準の設定にはデータの分散やサンプルサイズも影響するため、統計的な視点から総合的に判断することが求められます。

有意水準に関するトピックと注意点
有意水準は統計分析において重要な役割を果たしますが、正確に理解し、適切に解釈することが必要です。ここでは、有意水準を上回る場合と下回る場合の解釈、有意水準と危険率の違い、有意水準が満たされない場合の対応方法について詳しく説明します。これらのトピックを理解することで、統計分析の信頼性を高め、誤った結論を避けることができます。
有意水準を上回る場合と下回る場合の解釈
統計分析において、有意水準は観察結果の評価基準として非常に重要な役割を果たします。p値が有意水準を上回る場合、それは「帰無仮説が棄却されない」ことを意味し、観察された差異は偶然による可能性が高いと判断されます。一方、p値が有意水準を下回る場合、その結果は「有意である」と見なし、帰無仮説は棄却されることになります。例えば、5%水準を設定している場合、p値が0.05を下回ることでその観察結果は「有意」と判断されます。この解釈は、研究の信頼性を確保するために重要です。
有意水準と危険率の違いについて
有意水準と危険率は似ているようで異なる概念です。有意水準は、統計検定を行う際の棄却基準を示し、具体的には観察結果が偶然に起こる確率の上限を表します。一般的に5%または1%が使われ、「水準で有意」となる基準です。一方、危険率は第一種過誤、つまり「実際には真である帰無仮説を誤って棄却する確率」を意味します。したがって、有意水準が低いほど危険率も低くなり、検定結果の信頼性が高まります。これらの違いを理解することで、統計結果の解釈がより正確になります。
有意水準が満たされない場合の対応方法
有意水準が満たされない場合、つまりp値が設定した有意水準を下回らない場合には、帰無仮説は棄却されず、その結果は偶然によるものであると判断されます。しかし、これがデータの品質やサンプルサイズ、分析方法の見直しを必要とする目安となることもあります。たとえば、サンプルサイズが小さい場合、統計的パワーが不足し、有意差を検出できないことがあります。このような場合には、サンプルサイズの増加や、異なる統計手法の適用などの対応策を検討することが推奨されます。