カイ二乗検定とは

カイ二乗検定とは
カイ二乗検定とは、カイ二乗分布を利用する検定方法の総称です。
カイ二乗検定をすることによって、集計結果に出た差が偶然であるのか、そうでないのかを統計的に確認することができます。名義尺度のデータに対する検定としてよく使われます。
※名義尺度とは複数のカテゴリに分類するだけの尺度です。回答された数値は、意味の違いを区別するための数字であり、数値の大小に意味はありません。たとえば、性別の質問に対して「1:男性、2:女性、3:その他」という回答だったり、よく利用するコンビニは?という質問に対して「1:セブンイレブン、2:ファミリマート、3:ローソン、4:ミニストップ」という回答などが挙げられます。
カイ二乗検定の大まかな流れとしては、
①データの種類が質的データ(名義尺度)であることを確認する。
②データの種類が度数の総和であること(累積頻度)を確認する。
③期待度数を計算する。
④カイ二乗検定を行う。
カイ二乗検定が利用されるケースとして「適合度の検定」と「独立性の検定」の2種類があります。この2つについて例題をとおして詳しく紹介していきます。

適合度の検定 -解説と計算方法-
この検定では、観測度数(実際に得られた度数)と期待度数(帰無仮説のもとに計算された度数)が適合しているかを調べることができます。
A高校160人の「よく利用するコンビニ」の結果をまとめた数字が表1です。

特定のデータが複数のカテゴリに分類されたとき(今回だとセブンからミニストップまでの4分類)、何かしら比率に対する仮説の設定をされていることが、適合度の検定をするときに必要になります。
たとえば、よく利用するコンビニにおいて全カテゴリの度数が等しい」という仮説があったとき、それは「各カテゴリの度数に偏りがない」と言い換えられます。
この仮説を表すと表2のようになります。160人が偏りなく分類されるので、各カテゴリ40人ずつとなります。
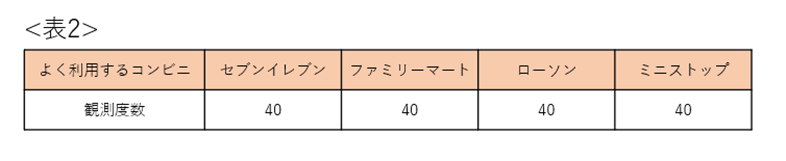
実際に得られた度数を観測度数と言うのに対して、仮説通りに考えて帰無仮説の元、期待される度数を期待度数と言います。(ここでは、偏りがないという帰無仮説の元、160人が各カテゴリ40人ずつ分類されることが期待されるので期待度数は40となります。)
「各カテゴリの度数に偏りがない」という仮説を帰無仮説とする検定を適合度の検定と言います。
この手法は、観測度数(実際に得られた度数)と期待度数(帰無仮説のもとに計算された度数)がマッチしているか、適合しているかを調べることができます。
この検定では、検定統計量を以下のように定めます。
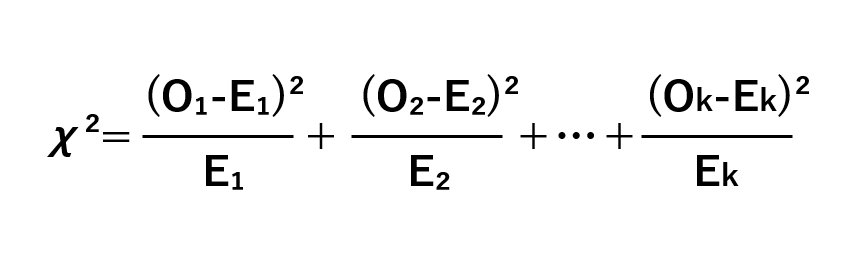
この場合、O₁,O₂,…,Okは観測度数を表します。Oとは「観測された」のobservedのOです。kとはカテゴリー数を表します。
一方、E₁,E₂,…,Ekは期待度数を表します。Eとは「期待された」を意味するexpectedのEです。
Ekは総度数に帰無仮説のもとでのカテゴリKの比率をかけることで求めることができます。
χ²という検定統計量は「観測度数と期待度数の間のずれを評価するもの」と言えます。実際の観測度数と期待度数の差が大きければ大きいほど、現実と期待のズレが大きく、χ²値は大きな値をとります。先ほどの式を見ても、OとEの差が大きいほど分子が大きくなり、全体の値が大きくなることが分かります。
このχ²という検定統計量は、自由度df-k-1(カテゴリー数-1)のカイ二乗分布に従うとされています。(カイ二乗分布はt分布と同様に確率分布の一つです。自由度によって分布の形が変わります。)
上記の方法を用いて以下の練習問題を解いてみましょう。
適合度の検定の練習問題
A高校の学生から無作為に160人を選び、よく利用するコンビニをアンケートしたところ、表1のような結果となりました。人数に偏りがあると言えるでしょうか。有意水準5%で検定してください。
1.帰無仮説と対立仮説の設定
帰無仮説H₀:人数に偏りがない
対立仮説H₁:人数に偏りがある
2.検定統計量の選択
χ²=(O₁-E₁)²/E₁+(O₂-E₂)²/E₂+…+(Ok-Ek)²/Ek
を検定統計量とする。
3.有意水準αの決定
5% つまり、α=0.05とする。
4.検定統計量の実現地を求めるには
まず、期待度数を求める。
4つのカテゴリに偏りがないとすると4等分すればいいので、それぞれの比率は0.25となる。総度数の160に0.25をかけると40。帰無仮説が正しければ、4つのカテゴリに偏りがないということであり、30人ずつになることが期待されるという意味となる。
次に、観測度数と期待度数をあてはめて、検定統計量の実現値を計算する。
χ²=(72-40)²/40+(50-40)²/40+(22-40)²/40+(16-40)²/40=50.6となる。
5.帰無仮説の棄却または採択の決定
4.で求めたχ²値が、自由度df=k-1=4-1=3のカイ二乗分布に従うことを利用し、棄却域を求める。カイ二乗分布表(https://home.hiroshima-u.ac.jp/ichi/chi-square-distribution.pdf)によると、自由度3における臨値(この値以上であれば棄却域となる境目の値の事)は有意水準5%で7.815である。(URL先だと、3と書かれている行と0.05が交差する場所m7.8147)よって、棄却域はχ²≧7.815となる。検定統計量の実現地は50.6であるため、棄却域に入るので帰無仮説は棄却される。
結果として、「A高校において、よく使うコンビニは有意に偏りがある」ということになる。※論文等では、χ²(1)=12.12, p<.05と表記されることもある。カッコ内の数字は自由度を表す。今回の例だと3。
この検定を行うことで、よく使うコンビニの比率に偏りがあることが分かる。
独立性の検定 -解説と計算方法-
この検定は2つの質的変数が独立であるか(あるいは連関があるか)を確かめるために行います。2つの質的変数が独立しているというのは、2つの質的変数に連関がないということです。2つの質的変数間の連関を調べるためにカイ二乗検定を行うことができます。
χ²値によって、観測度数と期待度数の間のズレを評価します。
2×2のクロス集計表があったとき、Aのカテゴリの違いによって(A₁かA₂)によって、B₁とB₂の度数の比が変わらないとすると、a:b=c:dということになります。そのため、比率を使って期待度数を求めることができます。
ただ簡単な方法として、列と行の周辺度数同士をかけて、総度数で割ると、期待度数を出すことができます。(例. aの期待度数は(a+b)(a+c)/(a+b+c+d)で求められる。)
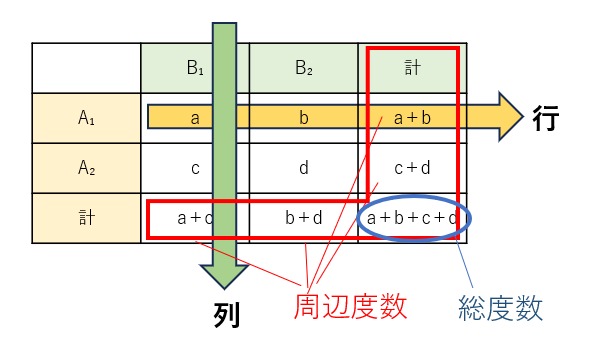
文字ではイメージしずらいと思うので、
この方法を用いて以下の練習問題を解いてみましょう。
独立性の検定の練習問題
成人の母集団から、300人の無作為標本を抽出しました。
全員に性別と日常の喫煙習慣の有無を尋ねた結果が表3のクロス集計表です。
この表の結果から、性別と喫煙習慣の独立性について、有意水準5%で検定してください。
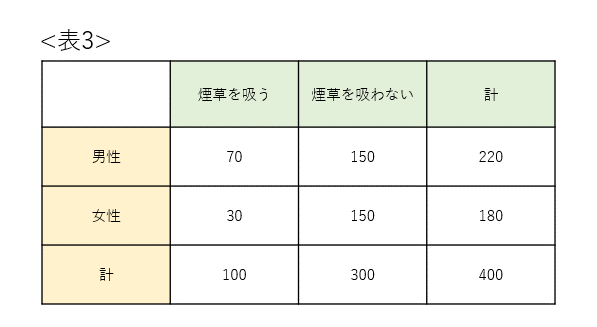
性別の違いによって、喫煙習慣の有無の碑率に差があるか考えていくことが必要となります。検定統計量は、χ²です。
χ²=(O₁-E₁)²/E₁+(O₂-E₂)²/E₂+…+(Ok-Ek)²/Ek
1.帰無仮説と対立仮説の設定
H₀:性別によって、喫煙習慣の有無が異ならない。すばわち、2つの変数は独立である。
H₁:性別によって、喫煙習慣の有無が異なる。すばわち、2つの変数には連関がある。
2.検定統計量の選択
χ²=(O₁-E₁)²/E₁+(O₂-E₂)²/E₂+…+(Ok-Ek)²/Ek
を検定統計量とする。
3.有意水準αの決定
5% つまり、α=0.05とする。
4.検定統計量の実現値を求める
まずは期待度数を求める。
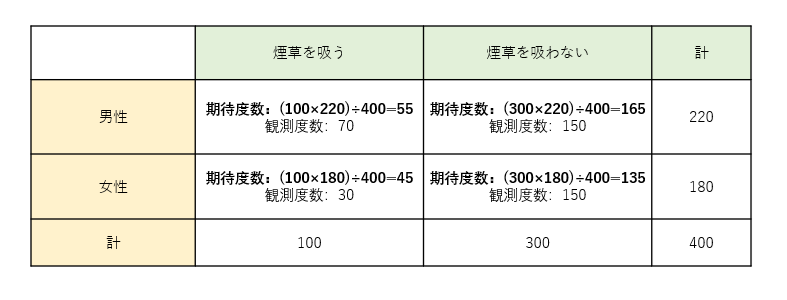
χ²=(70-55)²/55+(30-45)²/45+(150-165)²/165+(150-135)²/135=12.12
5.帰無仮説の棄却または採択の決定
クロス集計表からχ²値を計算するときは、自由度は(行数-1)×(列数-1)となる。今回のような場合は2×2のクロス集計表では自由度は(2-1)×(2-1)=1となる。
α=0.05, 自由度1のχ²値をカイ二乗分布表より求めると、臨界値は3.841であるので、棄却域はχ²≧3.841となる。検定統計量の実現地は12.12であるため、棄却域に入るので帰無仮説は棄却される。
結果として、性別と喫煙習慣の有無は独立ではなく、2つの変数の間には連関があるということになる。※論文等では、χ²(1)=12.12, p<.05と表記されることもある。
カイ二乗検定の弱点
このように便利なカイ二乗検定ですが、統計家のフランク・イェーツ氏は「カイ二乗値とカイ二乗分布に小さなズレがあり、そのズレの影響で本来より有意差が出やすく、実際よりは甘い結果になってしまうのではないか」と指摘しています。
※参考資料 「よくわかる心理統計」ミネルヴァ書房 山田剛史・村井潤一郎 著


