標準偏差(SD| standard deviation )とは
こんにちは。デジタルマーケティングカンパニー・オノフのshirayamaです。
データ分析や統計学の本に、必ず出てくる「標準偏差」という言葉。聞いたことはあっても、よくわからないという方は多いかと思います。
標準偏差は、統計学やデータ分析において不可欠な指標の一つです。データの散ら方やばらつきを定量的に示すもので、特に平均値だけでは捉えきれないデータの変動を理解するために重要な役割を果たします。標準偏差を求めることで、データの特性や傾向をよりよく把握でき、意思決定に寄与する情報を得ることが可能です。統計学を学習する際には、まずこの概念をしっかりと理解することが求められます。また、標準偏差はビジネスや品質管理、投資のリスク評価など多くの実務で活用されており、その利用範囲は広がっています。
今回は、標準偏差の意味や実際の活用シーンについて、わかりやすく解説していきます。
標準偏差とは
標準偏差とは、測定値のバラツキの度合いを表すために広く用いられています。
英語ではstandard deviationと表され、単語の頭文字をとってSDと表記されることもあります。
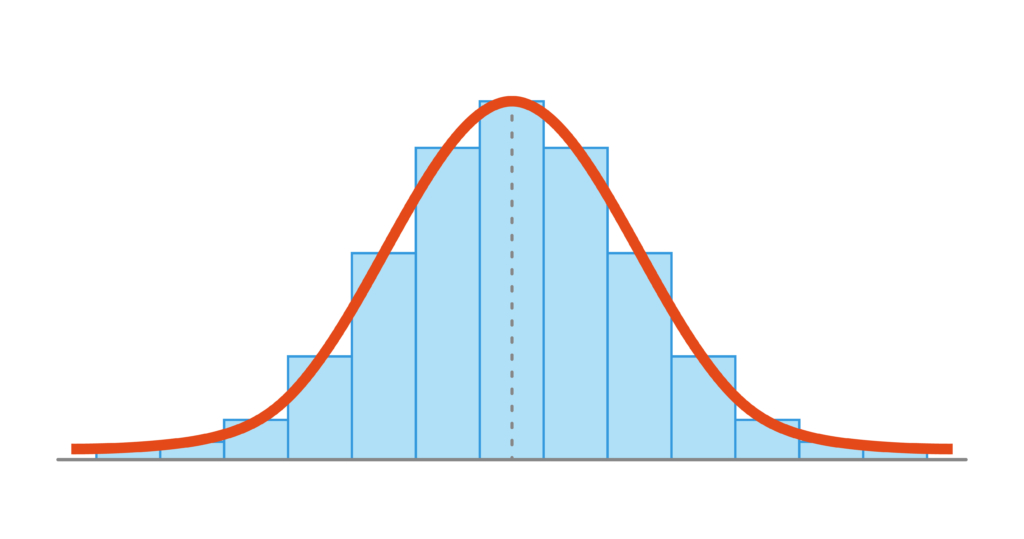
標準偏差が小さいということは全体のバラツキが小さいということ。つまり、測定値の分布が平均値の周りに集まっているということです。
また、逆に標準偏差が大きいということは、平均値から遠く離れている測定値が多くあることを意味します。
このように、標準偏差を通じてデータの分散の程度を把握し、判断材料として活用することができ、ビジネスの現場でも、これを基にした説明や分析が行われ、意思決定の精度向上をテスト的に図ることが求められます。

標準偏差の定義と計算方法
標準偏差の定義は、あるデータセットの各データが平均からどれくらい離れているか、その「平均からの距離」を示すものです。具体的な計算式としては、まずデータの平均を算出し、各データからその平均を引いて偏差を求めます。この偏差を二乗し、その平均を取り、最後に平方根を計算することで標準偏差が求められます。この計算手順に従うことで、データのばらつき具合が数値として得られ、具体的な状況を把握することができます。標準偏差は一般的に、データが正規分布に従っている場合に特に意味を持つ指標です。
標準偏差と分散の違い
標準偏差と分散は、どちらもデータのばらつきを表す指標ですが、その計算方法と解釈には重要な違いがあります。
標準偏差を知る上で重要なのが「分散」です。
標準偏差と分散は、データセットのばらつきを示す統計量ですが、計算方法や解釈において違いがあります。
計算方法としては以下の違いがあります。
分散(Variance)
分散とは、データの各値が平均からどの程度離れているか・対象データの散らばりの度合いを示す指標です。英語ではVarianceと表されます。分散が小さいほどデータの数値が平均値中心に集まっており、分散が大きいほど数値が平均値から離れていることを意味します。「分散」「標準偏差」もデータの広がり具合を表す指標の一つです。
分散の計算方法
計算方法としては、まず各データから平均値を引き二乗して、それらを合計します。そして、その合計した数を全体の数で割ります。
この際、偏差の二乗を使用するため、値が正の数として計算されます。しかし、分散の単位は元のデータの単位を二乗したものであるため、直感的な理解が難しいことが多いです。
分散が大きいほどデータが散らばっていますが、単位が元のデータと異なります。
標準偏差(Standard Deviation)
標準偏差は分散の平方根を取ったもので、元のデータと同じ単位で表されます。分散の平方根です。
標準偏差はデータのばらつき具合を直感的に把握するために非常に役立つ指標といえます。また、実務の場では標準偏差がよく用いられ、データ分析やリスク管理での意思決定に貢献しています。標準偏差は元のデータと同じ単位を持ち、分散よりも直感的に解釈しやすいです。標準偏差が大きいと、データがより広がっていることを示します。
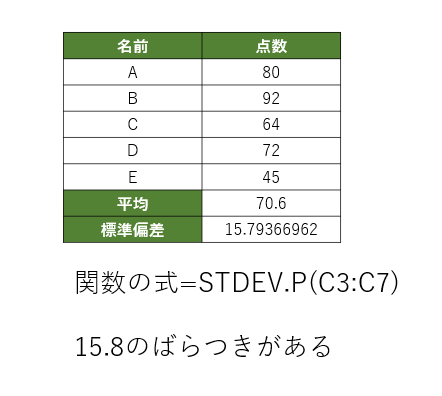
標準偏差の計算方法
標準偏差の計算方法は、まず、データの平均値を算出し、これを基にして各データから平均値を引いて偏差を求めます。次に、その偏差を二乗し、全ての二乗された値を合計します。この合計をデータの数で割ることで分散が求められ、最後にその平方根を取ることで標準偏差が得られます。
簡単に言えば、標準偏差は分散を単位について調整したものと考えることができます。
標準偏差の特徴
標準偏差は元の単位を保つため、データのばらつきを直感的に把握しやすい特徴があります。ビジネスの分野では、品質管理や販売予測、またはマーケットリスクの評価において標準偏差が頻繁に用いられます。特にデータが正規分布に従う場合には、標準偏差を利用した分析が有効であり、意思決定に貢献します。
標準偏差の活用シーン
標準偏差は、平均値などでは読み取れなかったデータの特徴も把握できるようになるため、さまざまな場面で活用されています。
品質管理
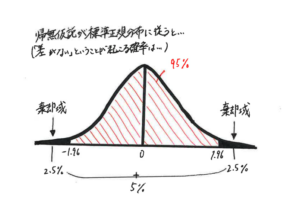
サイズや重さなど、商品の個体差をどの程度許容するかの予測を立てることができます。標準偏差には、平均値から標準偏差±2にデータの約95%が収まる特徴があります。この特徴を利用して、サイズや重さが平均値から±2以上外れたものを規格外とするなどをして品質を担保します。
品質管理において標準偏差は、製品のばらつきを継続的に把握するための重要な指標であり、製造工程で得られたデータを用いて標準偏差を計算することで、製品の品質の安定度を確認できます。
また標準偏差が大きくなると、製品が規格から外れるリスクが高まるため、この情報は製造工程を見直し、適切な統計的手法を取り入れるための根拠となります。
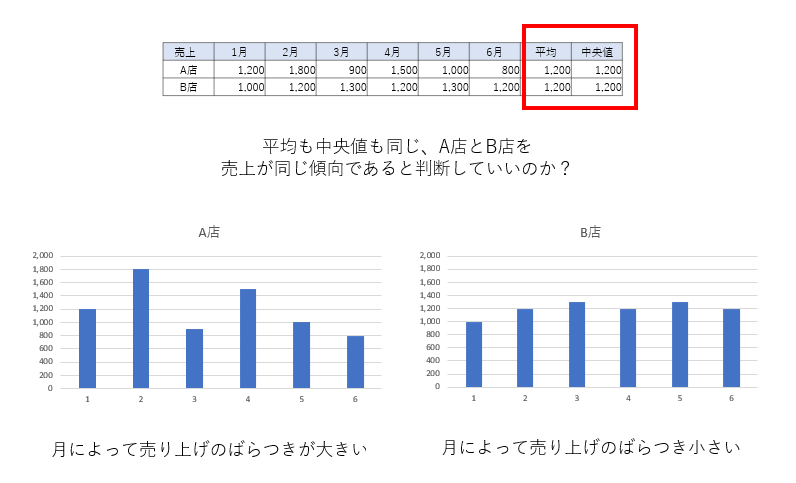
売上のばらつき具合を把握する
商品Aと商品Bがあり、Aの販売数の標準偏差は10、Bの標準偏差は100だったとします。AとBの販売数の平均値が同じだった場合、A商品は安定して売れていることがわかります。売上データの標準偏差を分析することで、売上のばらつきを明確に把握することができます。
これを応用すると業績の予想にも活用することができます。
投資のリスク評価
標準偏差は金融商品のリスクを数値化する際にも使われることがあります。
株式や資産のリターンを分析する際、標準偏差を計算することで、その投資のリスクを数値化できます。
投資信託の場合、ある一定の年数を設定し、騰落率の平均値を求め、リターンから平均値との差を年ごと求めます。それをさらに2乗して一定期間の年ごとの偏差を合計し、年数で割って平方根を出します。これがリターンとのブレを示す標準偏差となります。
たとえば、ある株式のリターンの標準偏差が高ければ、それは価格の変動が大きく、投資に対する不安要素が多いことを示します。逆に、低い場合は比較的安定したリターンが予想されます。この情報を基に、投資者は自身のリスク許容度に応じたポートフォリオの再構築が可能であり、より安全な投資戦略を策定できるのです。
標準偏差はリターンのばらつきを示すため、リスクの尺度として広く受け入れられています。
自分の学力を客観的に判断する
教育の分野においても、標準偏差は学力評価の重要な指標となります。
偏差値と呼ばれているもので、平均が異なるテストの点数を同じ指標で比較するために生み出されたものです。偏差値という言葉は認知度が非常に高いと思いますが、実は標準偏差がベースとなっています。偏差値は平均値が50となり、標準偏差1個分のずれに対して10の値を与えるという形を取ります。
標準偏差のデメリット
標準偏差はデータのばらつきを示す重要な指標ですが、いくつかのデメリットも存在します。長所と短所を理解し、他の指標や分析と組み合わせることで、より包括的なリスク評価や分析が可能となります。
標準偏差の短所として、以下が挙げられます。
正規分布が正しいことが大前提となっている
1つ目のデメリットは、標準偏差が正規分布に依存していることです。
データが正規分布に基づいている結果、平均と標準偏差のみで大部分をカバーすることが可能ですが、実際のビジネスや実務のデータは必ずしも正規分布に従うわけではないため、過去のパフォーマンスが将来にどれだけ適用可能かは不確かです。偏差が大きくなる場合、データの分布が不均一であるため、正確な分析が難しくなります。このような状況では、標準偏差だけに頼ると誤解を招く恐れがあります。
標準偏差が有効に機能するためには、データが正規分布に従う必要があります。正規分布が成り立つ場合、標準偏差を利用してほとんどのデータの位置を明確に把握することが可能です。
データを理解するためには、他の指標を併用することをお勧めします。
外れ値の影響を受けやすい
極端な価格変動(外れ値)がある場合、標準偏差は影響を受けやすく、ポートフォリオの実際のリスクを過大または過小に評価する可能性があります。外れ値とは、他のデータから著しく離れた値を指し、これが標準偏差に与える影響は無視できません。
高い値や低い値が含まれると、全体の分散が不自然に増加し、その結果、標準偏差も誤った大きさになります。このような影響を最小限に抑えるために、データセットから外れ値を事前に取り除く方法が一般的です。また、外れ値を特定するための手法として、箱ひげ図やZスコアを活用することが推奨されます。これにより、標準偏差をより正確に算出することができ、データの信頼性を高めることが可能です。

最後に
以上、標準偏差について解説させて頂きましたが、お役に立ちましたでしょうか。
標準偏差はデータのばらつきを示す指標の1つで、その名が示すように標準化されているのが特徴です。そのため、平均が同じ集団のばらつきを同じ土俵で比較できます。また、在庫管理や品質管理など、さまざまな場面で活用されています。
標準偏差の正しい活用方法などをこの記事で再度確認いただき、一度実践してみて頂けると嬉しいです!

