加重平均とは?算術平均との違いや使い分けをわかりやすく簡単に解説!
デジタルマーケティングカンパニー・オノフのnagaiです。
加重平均は、異なる重み(ウエイト)を加味した平均の算出方法です。通常の平均値を求める際には、すべてのデータを足してデータの数で割りますが、加重平均ではデータごとに異なる重要度を考慮します。これにより、データが持つ意味を正確に反映させることが可能となります。特に、数量の大きさや影響力が異なる場合において、加重平均を用いることで、より現実に即した結果を得られる場合があります。職場での売上分析や教育現場における成績評価など、さまざまな場面で重宝される手法と言えるでしょう。
今回は加重平均についてわかりやすくご説明いたします!
加重平均とは
加重平均とは、特定のデータに対して重要度を付与して算出する平均値です。平均値とは分布するデータの中間に位置する数値のことで、加重平均のほか算術平均や幾何平均(相乗平均)、二重平均などの種類があります。単純な平均では、「算術平均」が用いられることが多く、全てのデータが同等の価値として扱われますが、加重平均では個々のデータが持つ性質や影響を踏まえて計算を行います。そのため、データの重要度が異なる場合には非常に有効な方法です。例えば単価の異なる商品の販売実績から平均単価を求める場合や、異なる人数で構成されるクラスの平均身長から学年全体の平均身長を求めたい場合、また、学生の成績評価の際に課題やテストの評価基準が異なる場合など、データによって重要度が異なるときは、単純にすべての点数を平均する算術平均ではなく、各評価に重みを付けて計算する加重平均で考える方が実情を反映します。これにより、加重平均はデータ分析や結果の解釈をより精緻に行うことができる手法となっています。
算術平均については、「リサーチにおける平均値・中央値・最頻値とは」をご覧ください。
加重平均の定義と基本概念
加重平均は、値ごとに設定された重みを考慮して平均値を計算する手法と定義されています。この手法では、各値にその値の重要度や影響度を示す重みを掛けて合計し、その合計を重みの合計で割ることで加重平均を求めます。このプロセスは、異なる性質を持つデータを一つの指標としてまとめる際に役立ちます。たとえば、試験の結果を評価する際、各科目の配点が異なるため、それぞれに対し異なる重みを設けて計算を行うと、より公平な評価が可能になります。つまり、加重平均は単純な算術平均とは異なり、データの本質をより適切に表現するための手法と言えるでしょう。
算術平均と加重平均の違い
算術平均と加重平均の違いは、主にデータの扱い方にあります。算術平均は、データの合計をデータ数で割ることで求めるシンプルな方法ですが、すべてのデータを同等に扱うため、実際の重要度や影響を反映することができません。一方で、加重平均は、各データに異なる重みを与えることで、より現実的な平均値を算出します。このため、特定のデータが他よりも重要な場合、加重平均を使用することが望ましいと言えます。たとえば、商品の販売実績を分析する際に、販売数が多い商品をより重視して評価したい場合、加重平均が効果的です。このように、状況と目的に応じて算術平均と加重平均を使い分けることが重要です。

加重平均の計算方法
加重平均の計算は、データの重みを正確に反映させた平均値を求めるための手法です。この手法では、各数値にその値の重みを掛け、その合計を全ての重みの合計で割ります。具体的な計算手順としては、最初に各データの値と重みを用意し、それぞれを掛け算して合計を算出します。次に、全ての重みを合計し、最初に算出した合計をこの重みの合計で割ることで加重平均が得られます。この方法は、売上や成績などのデータが異なる重要性を持つ場合に特に効果的です。あとで解説するエクセルを用いた計算方法も、手動での計算にかかる手間を省くことができ、効率的に加重平均の計算を行うことが可能です。
加重平均の数式と計算手順
加重平均の数式は、与えられたデータセットの各値に重みを掛けた合計を、全ての重みの合計で割ることに基づいています。具体的には、加重平均は次のように表現されます。まず、x₁,x₂,…,xₙをデータの値、w₁,w₂,…,wₙをそれぞれの重みとすると、加重平均は次の式で計算されます。加重平均=(x₁w₁+x₂w₂+…+xₙwₙ)/(w₁+w₂+…+wₙ)。この数式は、様々なデータにごくわずかな違いがある場合でも、より正確な平均を求めることを実現します。また計算手順としては、まず各データとその重みを掛け、次にそれらの合計を重みの合計で割ることで結果を得られます。
加重平均をエクセルで計算する方法
エクセルを活用すれば、加重平均の計算を迅速かつ正確に行うことが可能です。具体的には、エクセルの関数や機能を利用して、計算手順を簡素化することができます。一般的には、SUMPRODUCT関数を使用することで、各値と重みを掛けて得た合計を速やかに求めることが可能です。この関数を使うことで手動で計算する時間を短縮し、データ数が多い場合でもスムーズに処理できます。さらに、SUM関数を使用して重みの合計を取得し、これを利用して加重平均を算出することで、より効率的な作業が実現します。エクセルを用いることで、正確な計算をスピーディに行うことが可能です。
SUMPRODUCT関数を使った計算方法
SUMPRODUCT関数は、エクセルでの加重平均を算出する際に非常に便利な機能です。この関数は、指定した範囲のセルにある数値を掛け合わせ、その総和を計算するものです。たとえば、商品の価格と販売数から平均単価を求める場合、商品ごとの価格と販売数を各々のセルに入力し、それらをSUMPRODUCT関数に渡すことで、手動で計算することなく簡潔な結果を得ることができます。このような方法により、時間を大幅に節約しつつ、正確な加重平均の計算が行えるため、業務の効率化にも寄与します。特にデータが多い場合や複雑な計算が必要な時に、その効果は顕著に現れます。
データの合計で割る手順
加重平均の計算を完了させるためには、まず求めた合計を全ての重みの合計で割る必要があります。これは、計算した値が正確な平均となるために欠かせないステップです。エクセルではこの作業も簡単に行えます。SUM関数を使用して、各データに関連する重みの合計を取得し、その値を先ほど算出した合計で割ることで、正式な加重平均が得られます。このプロセスにより、正確なデータ分析が可能となります。特にビジネスや学業において、情報量が多い場合、こうした効率的な方法を採用することで、分析結果の信頼性を高めることが期待されます。
具体例で学ぶ加重平均の使い方
加重平均の使い方は多岐にわたり、特にデータの重要度や影響度が異なる場面で活躍します。実際のビジネスや学術的な調査において、正確な数値を導き出すために加重平均が利用される事例は数多く存在します。例えば、アンケートを基にした調査では、参加者の回答結果に基づく満足度を算出する際、各回答に対して異なる重みを設定することが可能です。このような使い方によって、データの偏りを減少させることができ、より信頼性の高い分析結果を得ることができます。今後の取り組みに向けて、実例を通じて加重平均の理解を深めることが重要です。
アンケートで加重平均を用いる事例
アンケート調査において加重平均は非常に効果的です。例えば、ある企業が新商品の満足度調査を実施した際、5段階評価での意見収集を行うことがあります。満足・やや満足・普通・やや不満・不満の回答に対して、参加者数や重要度に応じて重みを設定し、計算を行います。具体的には、各選択肢に対し、それぞれの実回答数を掛け合わせ、合計を全体の参加者数で割ることで、全体の満足度を算出します。この方法を用いることで、実際のユーザーの意見をより正確に反映したスコアを得ることが可能になり、商品の改良やマーケティング戦略に役立たせることが期待できます。
例題
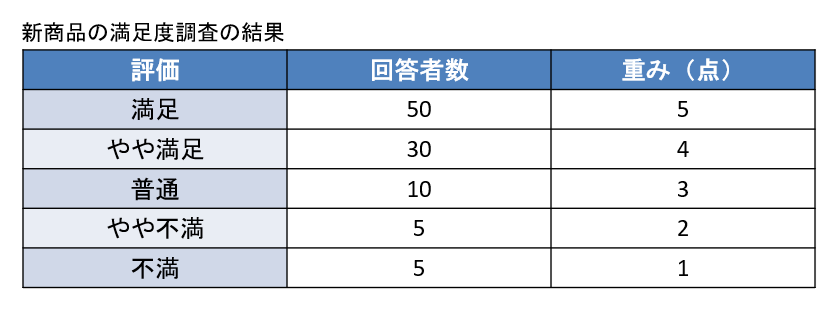
ある企業が新商品の満足度を調査し、以下のような5段階評価の結果を得ました。
計算手順
- 各回答の点数と回答者数を掛け合わせ、合計を求めます
- (50 × 5) + (30 × 4) + (10 × 3) + (5 × 2) + (5 × 1) = 370
- 全体の回答者数で割ります
- 370 ÷ (50 + 30 + 10 + 5 + 5) = 3.7
解説
この満足度スコア3.7は、全体の参加者の意見を反映した平均的な満足度を示します。
このように加重平均を使うことで、回答の偏りや重要度を考慮した分析が可能になり、マーケティング戦略の立案や商品の改善に活かせます。
売上における加重平均の適用例
ビジネスシーンでは、売上データを基にした加重平均の適用も重要です。例えば、商品A、B、Cの異なる価格帯での売上がある場合、それぞれの商品の販売数量を加味して、平均単価を求めることが求められます。商品ごとの売上額を各商品の販売数量で割り算し、その結果を重みとして加重平均を計算します。この結果により、業績評価において価格設定や在庫戦略の見直しが行え、より効果的な販売計画を立てることができるのです。売上データを分析する中で、加重平均の利用は企業にとって戦略的な意思決定を促進するツールとなります。
複数の要素を含むデータでの活用
複数の要素が絡み合うデータの分析においても、加重平均が役立ちます。たとえば、学生の成績を評価する場合、試験の成績だけでなく、課題、参加態度なども考慮する必要があります。このような状況では、各評価項目に重みを付けて加重平均を算出することが有効です。生徒の成績、授業への参加状況、提出物の評価などに応じて、異なる重みを設定し、全体のパフォーマンススコアを算出することで、より公正かつ具体的な結果を出すことができます。このアプローチは、教育機関や企業においても、評価制度の透明性を高めるために非常に重要です。
加重平均と算術平均の使い分け方
加重平均と算術平均の使い分けは、データの性質や求めたい結果によって異なります。算術平均は、全てのデータを同等に扱い、単純に総和をデータ数で割ることで算出されますが、これでは重要度の異なるデータを適切に反映できないことがあります。特に、データが異なる影響を持つ場合には、加重平均を利用することで、より実情に即した結果を得ることが可能です。例えば、試験や評価において、異なる科目の配点が異なる場合、加重平均を使用して各科目の重要性を反映させることで、正確な成果が得られることが期待されます。
使い分けの場面とポイント
平均と加重平均の使い分けは、具体的な状況に応じて行う必要があります。算術平均が適している場面としては、データが均等に重要であり、個々の影響度に差がない場合が挙げられます。例えば、簡単なクラス内テストの成績を求める際には、算術平均が効果的です。一方、加重平均は、データの重要度が異なるケースに非常に有用です。たとえば、学生の成績評価において、試験、課題、参加態度など、それぞれの項目の配点が異なる場合、加重平均を適用することで、より公正かつ正確な評価を実現できます。したがって、データの特性に応じて最適な手法を選択することが重要です。
加重平均のメリットと適用範囲
加重平均のメリットは、データの異なる重要度や影響を考慮に入れた平均値を提供できる点です。この手法を用いることで、個々のデータが持つ意味をきちんと反映しながら結果を導き出すことが可能です。特に、ビジネスの売上分析や学業の成績評価において、加重平均は活用されることが多いです。また、加重平均は異なる分野で広く適用されており、特にマーケティング調査や製品評価など、情報収集の場面でもよく利用されます。データの性質に対する理解を深め、その特性を踏まえた上で加重平均を適用することで、より有意義な結論を導くことができます。
まとめ
加重平均は、データの重要度に応じて異なる重みを考慮に入れた計算方法であり、非常に実用性が高い手法です。特にデータの重要性が異なる場合、加重平均を用いることで、より正確な結果を導き出すことが可能です。この手法は、ビジネスや学術研究、マーケティング調査など、さまざまな分野で幅広く利用されています。算術平均と異なり、個々のデータに適切な価値を付与し、全体像をより具体的に把握する際に役立つため、適切な場面を見極めることが重要です。加重平均の正しい理解とその活用法を習得することで、データ分析の精度向上が期待でき、意思決定においてもより確かな根拠を持つことができると言えます。

